February 2021, Duelund loudspeaker crossover design
General
The Duelund filter has been created by Steen Duelund. His arguments to choose this type of filter are described in his article “The art of building a loudspeaker to the end”
It is a crossover approach that the filter functions of the different speaker ways remain in phase at all frequencies. The sum response has an all pass filter behaviour.
Some parameters can be chosen to define the filter type. Parameter ‘a’ determines the damping of the second order filter sections. The order can be chosen to define the slope of the curves in the stop band of the different ways.
In this study the 4th order and 8th order Duelund filter for different values of parameter a are described. Some examples show some interesting concepts to make a multiway loudspeaker crossover.
4th order Duelund filter
Duelund 4th order sum polynomial
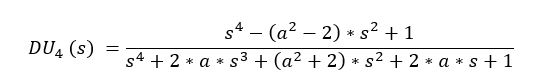
This polynomial is obtained by multiplying two second order all pass sum responses.
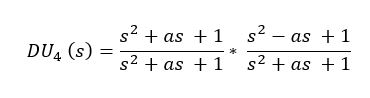
Remark that all these functions are normalized to wn = 1 rad/sec. To obtain the function at other values of wn, all the s variables have to be divided by wn.
By multiplying second order allpass functions, the amplitiude of the 4th order polynomial is also allpass. The amplitude is equal to 1, the phase response becomes different. Parameter ‘a’ determines the damping of the second order sections. If ‘a’ is chosen 2 or more, the second order functions become critical damped. There is no overshoot in the impulse response or peaking in the groupdelay anymore.
This 4th order Duelund sum response can be realized with three sections.

Interesting Duelund 4th order examples for 3-way crossovers
Some examples of Duelund 4th order filters are described with different values for the parameter ‘a’.
Parameter a = 3
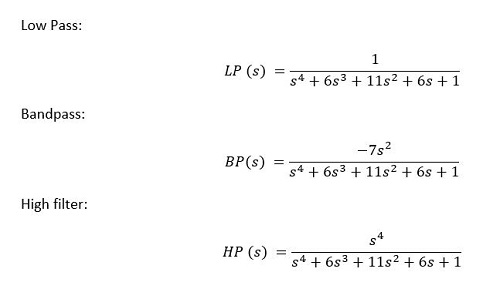
Example: 4th order Duelund filter, a = 3, fn = 1000 Hz and the sum response amplitude equal to 90 dB
Amplitude
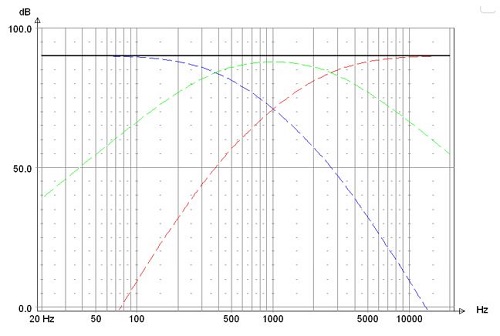
Frequencies f1 and f2 are the crossover frequencies. The ratio f2/f1 = 6.
Impulse Response
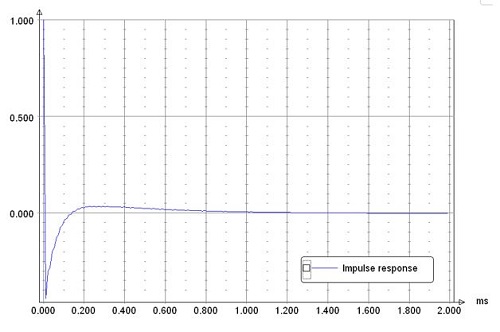
No impulse response overshoot.
Group Delay
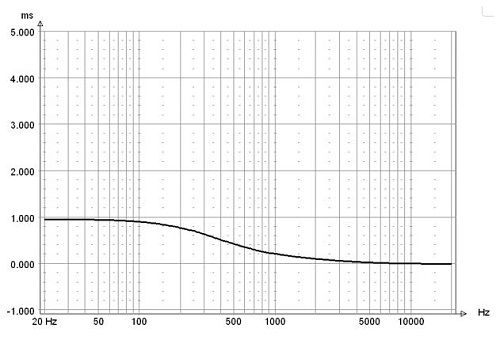
No group delay peaking.
Parameter a = 4

Example: 4th order Duelund filter, a = 4, fn = 1000 Hz and the sum response amplitude equal to 90 dB
Amplitude
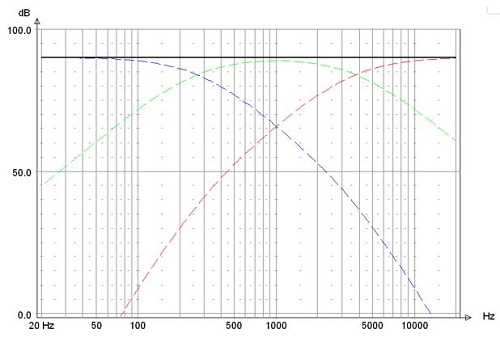
Frequencies f1 and f2 are the crossover frequencies. The ratio f2/f1 = 14.
Impulse response
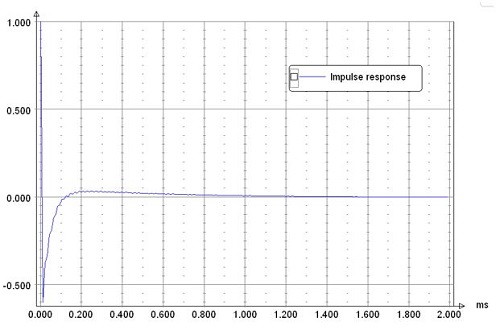
No impulse response overshoot.
Group Delay
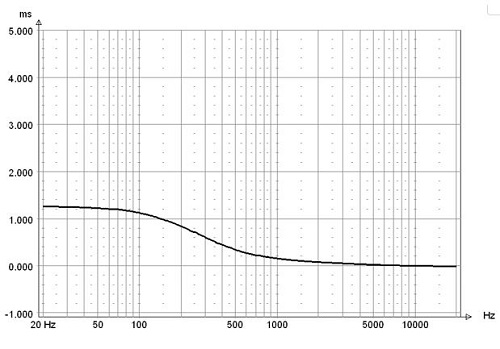
No group delay peaking.
8th order Duelund filter
Duelund 8th order sum polynomial
This polynomial is obtained squaring the fourth order Duelund sum response.
Functions are normalized to wn = 1 rad/sec.

Like with the 4th order Duelund filter, parameter ‘a’ determines the behavior of the 8th order Duelund filter. The low pass and the high pass filters have a 8th order slope in the stopband. Due to the high damping of the second order all pass sections the slope is 4th order in the first part of the stopband. The bandpass slopes in the two stopbands are 2nd order.
Interesting Duelund 8th order examples for 3-way crossovers
Some examples of Duelund 8th order filters are described with different values for the parameter ‘a’.
Parameter a = 2

Example: 8th order Duelund filter, a = 2, fn = 1000 Hz and the sum response amplitude equal to 90 dB
Amplitude
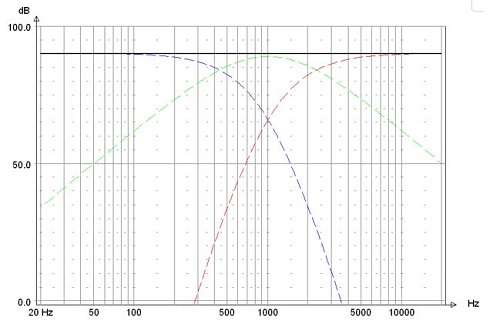
Frequencies f1 and f2 are the crossover frequencies. The ratio f2/f1 = 5.35.
Impulse response
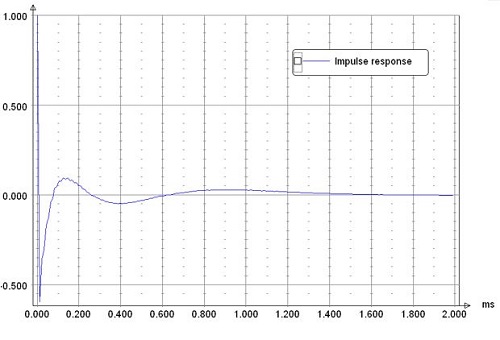
Some impulse response overshoot.
Group delay
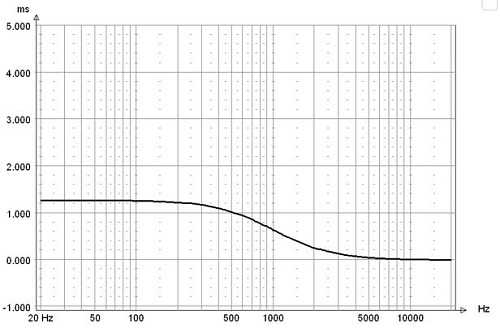
No group delay peaking.
Parameter a = 3

Example: 8th order Duelund filter, a = 3, fn = 1000 Hz and the sum response amplitude equal to 90 dB
Amplitude
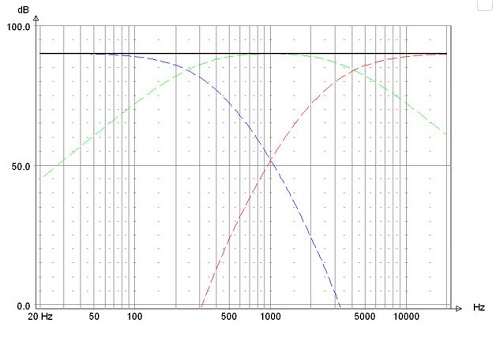
Frequencies f1 and f2 are the crossover frequencies. The ratio f2/f1 = 17.
Impulse response
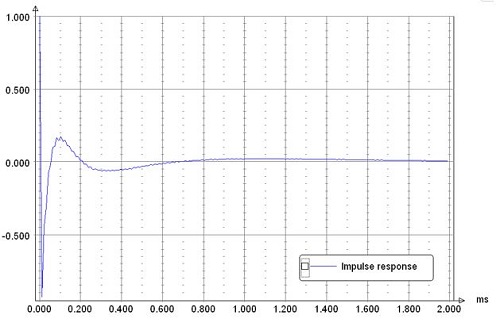
Some impulse response overshoot.
Group delay
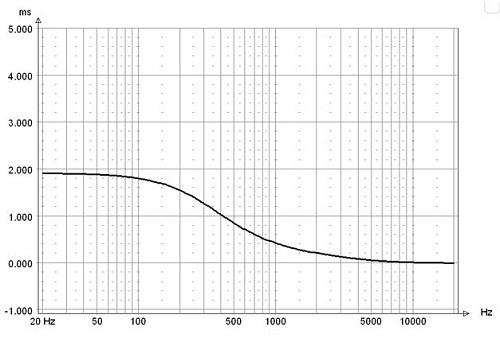
No group delay peaking.
